whx's Blog

see you

窝就复述下连接里的做法> < :http://recursion.is-programmer.com/posts/190037.html   

Orz。。。。

首先我们找出多少个点可以被覆盖。。。然后直接去掉那些不能被覆盖的。。剩下的点一定要被覆盖了

然后我们考虑按照一定的顺序来覆盖，由于是横着的一个长条，那么我们从左往右做

先考虑y>=R的情况

假设当前处理到了x=a，某个点没有被覆盖，那么我们要选一个圆（绿色）来覆盖它，而之前选的圆有两种情况（红色）：

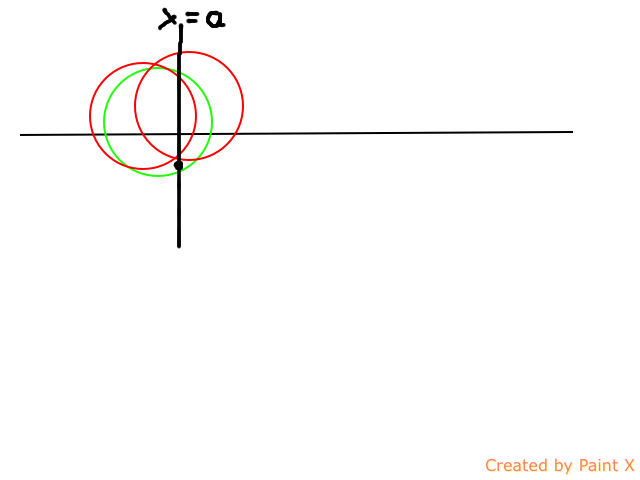
注意我们已经覆盖到x=a了，所以x=a之前的部分都没有用了，之后的部分里

左边的红色圆被绿色完全包含了，可以直接丢掉

右边的红色圆比较麻烦。。但是注意，它左边的部分被绿色完全包含了，那么在选绿色之前，我们可以不选它，而直接选绿色，然后到之后再选它。。

也就是说最优方案存在一个分配办法（把每个点分给某个圆），使得每个圆覆盖的点（当然是可以被覆盖的点），都是一个按照x排序后连续的区间

那么对于只有一边的情况，我们就可以f[i]表示1~i的点都被覆盖了的代价，转移的时候直接枚举一个能覆盖i+1的圆，看它最大能连续的覆盖到j，然后f[i]->f[j] O(n^2)

对于两边的情况呢。。？

每个圆覆盖的不再是一个连续的区间了。。但是把点分成上下两半来看，每边的圆覆盖的一定还是一个连续的区间

本来我们是一个区间直接转移的。。现在区间要划分之后才连续了。。

我们不妨在状态里存一下最后一个区间，一个点一个点转移

f[i][j][k]表示考虑到了第i个点，上面用的最后一个圆是j，下面用的最后一个圆是k的代价

如果i+1在j或者k内，直接转移

否则从上面或者下面新选一个圆，新开一个区间转移

那么这题就解决啦> <

总结一下的话，就是证明了一个性质：可以分配使得每个圆覆盖的连续之后，我们就可以在每次前一个圆不能覆盖了之后，选一个新的圆并且把原来的圆丢弃了（所以一个点要不要选新圆就只和上一个圆有关了）

证明的方法是，考察那个新圆之前的圆（不能覆盖当前的x=a这个点的===>要么x=a右侧被新圆完全覆盖，要么x=a左侧被新院完全覆盖)，然后就得到要么以后都不会用到之前的圆，要么以前不需要用到之前的圆，那么覆盖就连续了。。

窝记了70+条来着。。？窝决定搞完一个note发一个到这里！

欢迎大家催更 > <

当前进度 ：8.5/70

1.如果要找到二维矩形内所有点（k个），归并树（log^2n + k）比主席树(klogn。。线段树找到在哪些x坐标上有点，对每个x坐标开一个vector，然后在每个有点的vector里面二分一下)优。。  

 //find kth
   x = S = 0;
   dep(i,m,0){
     x ^= 1 << i;
     if (x < N && S + s[x] < k) //x <= N! 一定要记得判一下！
	S += s[x];
     else 
	x ^= 1 << i;
   }
   x++;

11.C(n,2)种约束（若干个不等），无法容斥，

  似乎是dp一下找出n个点、j个联通块方案数对答案的贡献之类的。。。。？

   TAT好像不会啊。。求教

 [Cerc2012]Non-boring sequences

Description

Input

Output

由于是权限题窝就贴下题面吧。。做法可以看hgr同学的博客（http://blog.csdn.net/geotcbrl/article/details/49797889）或者是tjz唐老师的博客。。

然而窝第一眼看到这个做法的时候和hgr一样，认为这个做法是暴力。。唐老师说可以证明，问了唐老师，唐老师表示这个其实是证明

$T(n)=\max\{T(k)+T(n-k)+\min(n,n-k)\}=O(nlogn)$

然后使用归纳法证明。。。

嗯。。的确可以这么做。。但是看上去是不是不太直观啊。。

于是窝想了一个（两个？）直观的证明，是这样的：

我们考虑每个对时间复杂度有贡献的下标，它一定属于两段中比较小的那一段，于是。。每次每个下标被算一次，它的所在块就会缩小一倍，那么显然每个下标的贡献就是$O(logn)$，它的总时间复杂度就是$O(nlogn)$

说到底，我们不断拆分这个过程，分开后就不会再合并，而且每次拆开的复杂度就是拆成的两个序列中较小的一个，很自然地想到把这个过程倒过来，那么这就是一个启发式合并的过程，显然时间复杂度就是$O(nlogn)$啦

感觉这个可以叫『启发式拆分』？233 总之要注意这样的做法不是暴力，相反复杂度还很优秀。。

首先中文题面错了，是切比雪夫距离，而不是曼哈顿距离

切比雪夫距离的话，我们就强制每个维度上都必须要有一个取到0点，注意若干个面必须有一个取到0没有若干个面都没有取到0好做，那么直接容斥转化为后者即可。

#include <iostream>
#include <cstdio>
#include <algorithm>
#define dep(i,a,b) for(int i = a; i >= b; i--)
#define rep(i,a,b) for(int i = a; i <= b; i++)
using namespace std;
const int M = 1000000007;
int pow(int a, int b, int c){
    int w = 1;
    for(;b;b >>= 1, a = 1LL * a * a % c) if (b & 1) w = 1LL * w * a % c;
    return w;
}
const int N = 1010;
int fac[N], inv[N];
int c(int n, int m){
    return 1LL * fac[n] * inv[m] % M * inv[n - m] % M;
}
int n;
int calc(int d){
    if (d == 0) return 1;
    int ans = 0, t = 1;
    rep(i,0,n){
        int tmp = 1LL * c(n,i) * pow(2, 1LL * pow(d, i, M - 1) * pow(d + 1, n - i, M - 1) % (M - 1), M) % M;
        ans += t * tmp, ans %= M;
        t = -t;
    }
    return ans;
}
void work(){
    int d; scanf("%d%d",&n,&d);
    int ans = (calc(d) - calc(d - 1)) % M;
    if (ans < 0) ans += M;
    printf("%d\n",ans);
}
int main(){
    fac[0] = 1; rep(i,1,1000) fac[i] = 1LL * fac[i - 1] * i % M;
    inv[1000] = pow(fac[1000], M - 2, M); dep(i,1000,1) inv[i - 1] = 1LL * inv[i] * i % M;
    int T; scanf("%d",&T);
    while (T--) work();
}

AC的第300题让我意识到自己还是不够强TAT

加油吧！至少是一个开始！

mato神犇教导我们，要勤写总结，善于总结。所以赶快总结一发

1.在比赛方面：

      在这段时间打了一场NOI和一场cf，教训大概有这些。

      1）比赛开始之后一定要冷静地把所有题目全部看一遍再开始想题！

      2）即使是简单题也一定要注意细节

      3）紧张虽然可能可以提高速度，但是更多的时候不仅会降低准确度和思维能力，还会导致低级的失误，一定不能紧张。

      4）比赛之后好好休息，不要颓废。

      5）即使是打算写暴力、乱搞或者骗分，也一定要认真地思考优化什么的。不能抱着“反正不是std能拿多少分是多少”的想法去写，万一AC了呢。（比如wzf的ahoi day1 t2）

      6）写有一定代码难度的代码之前一定要想想有没有比这个好写的办法，可能这就会带来时间的节省或者是一个WA变成AC

      7）写代码之前想好操作的细节，确保正确性。

      8）对于时间复杂度、一个方向是否可行，一定不能轻易否决，不能凭感觉丢弃想法，要仔细分析。

      9)  考挂了还是实力不足，技不如人，运气不够的背后是绝对实力不足，不要用yy自欺欺人欺骗自己。

2.在学习方面

      1）方法上

                 mato神犇教导我们：一，做杂题提升并不大，比赛可能更合适。二、学习应该多做专题训练。三、有脑洞一定要记录下来，

      2）知识点上

                窝在NOI回来之后，做了这些事：

                       1.在bzoj上做了一些dp的训练 和 数论的训练。

                               可能这个比较锻炼思维能力。dp里面 董爷题 和 那道字符串（见日常训练1）我开始没想出来，在树上f[i][j][k][2]的这种状态方式 和 f[i][j][k][l]表示i..j这一段能否变成[k][l]这个字符串上的状态，字符串上dp状态很多都是f[i][j][xxx]，表示i。。j变成。。。这样。

                       2.验了互测的题目，收获有：

                               并查集的root上可以维护一些东西，然后可以启发式合并

                               一种对付二分区间过长的倍增，有一种二分区间很长，初始[1..n]，然后一次check是O（len）的。你要求得一个ans之后，再对[ans, n]做这个二分，这就很不好。我们应用倍增的思路 check(l, l + 1) check(l, l + 2) check(l,l + 4).....这样下去，最长check区间只是2(ans - l).(令L = 2 * (ans - 1))这个check的过程是O(4L) = O(L)的，然后再在这个长为2L的 区间二分即可，这样总复杂度是O（nlogn）的

                      3.验了BC的题目，然而并不会做CD，这还没做完。

3.在态度方面

              受NOI滚粗影响，稍稍有些消沉，但是无论如何，明年再战！

              同时稍稍有些浮躁，我应该摆正心态，静下心来，读题、想题、写代码、总结。。。。

              OI，我是认真的。