whx's Blog

窝就复述下连接里的做法> < :http://recursion.is-programmer.com/posts/190037.html   

Orz。。。。

首先我们找出多少个点可以被覆盖。。。然后直接去掉那些不能被覆盖的。。剩下的点一定要被覆盖了

然后我们考虑按照一定的顺序来覆盖，由于是横着的一个长条，那么我们从左往右做

先考虑y>=R的情况

假设当前处理到了x=a，某个点没有被覆盖，那么我们要选一个圆（绿色）来覆盖它，而之前选的圆有两种情况（红色）：

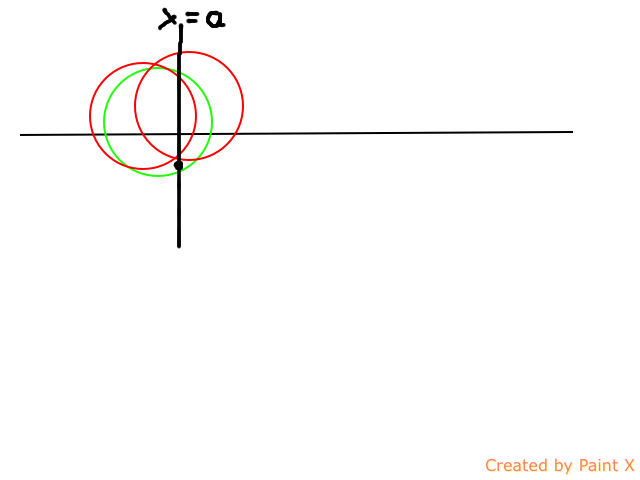
注意我们已经覆盖到x=a了，所以x=a之前的部分都没有用了，之后的部分里

左边的红色圆被绿色完全包含了，可以直接丢掉

右边的红色圆比较麻烦。。但是注意，它左边的部分被绿色完全包含了，那么在选绿色之前，我们可以不选它，而直接选绿色，然后到之后再选它。。

也就是说最优方案存在一个分配办法（把每个点分给某个圆），使得每个圆覆盖的点（当然是可以被覆盖的点），都是一个按照x排序后连续的区间

那么对于只有一边的情况，我们就可以f[i]表示1~i的点都被覆盖了的代价，转移的时候直接枚举一个能覆盖i+1的圆，看它最大能连续的覆盖到j，然后f[i]->f[j] O(n^2)

对于两边的情况呢。。？

每个圆覆盖的不再是一个连续的区间了。。但是把点分成上下两半来看，每边的圆覆盖的一定还是一个连续的区间

本来我们是一个区间直接转移的。。现在区间要划分之后才连续了。。

我们不妨在状态里存一下最后一个区间，一个点一个点转移

f[i][j][k]表示考虑到了第i个点，上面用的最后一个圆是j，下面用的最后一个圆是k的代价

如果i+1在j或者k内，直接转移

否则从上面或者下面新选一个圆，新开一个区间转移

那么这题就解决啦> <

总结一下的话，就是证明了一个性质：可以分配使得每个圆覆盖的连续之后，我们就可以在每次前一个圆不能覆盖了之后，选一个新的圆并且把原来的圆丢弃了（所以一个点要不要选新圆就只和上一个圆有关了）

证明的方法是，考察那个新圆之前的圆（不能覆盖当前的x=a这个点的===>要么x=a右侧被新圆完全覆盖，要么x=a左侧被新院完全覆盖)，然后就得到要么以后都不会用到之前的圆，要么以前不需要用到之前的圆，那么覆盖就连续了。。