24
2016
- 未命名 -
20
2016
bzoj4092幻想乡Wifi搭建计划
窝就复述下连接里的做法> < :http://recursion.is-programmer.com/posts/190037.html
Orz。。。。
首先我们找出多少个点可以被覆盖。。。然后直接去掉那些不能被覆盖的。。剩下的点一定要被覆盖了
然后我们考虑按照一定的顺序来覆盖,由于是横着的一个长条,那么我们从左往右做
先考虑y>=R的情况
假设当前处理到了x=a,某个点没有被覆盖,那么我们要选一个圆(绿色)来覆盖它,而之前选的圆有两种情况(红色):
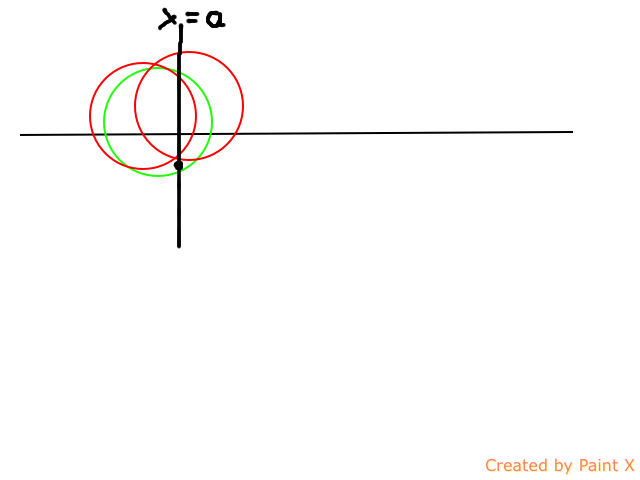
注意我们已经覆盖到x=a了,所以x=a之前的部分都没有用了,之后的部分里
左边的红色圆被绿色完全包含了,可以直接丢掉
右边的红色圆比较麻烦。。但是注意,它左边的部分被绿色完全包含了,那么在选绿色之前,我们可以不选它,而直接选绿色,然后到之后再选它。。
也就是说最优方案存在一个分配办法(把每个点分给某个圆),使得每个圆覆盖的点(当然是可以被覆盖的点),都是一个按照x排序后连续的区间
那么对于只有一边的情况,我们就可以f[i]表示1~i的点都被覆盖了的代价,转移的时候直接枚举一个能覆盖i+1的圆,看它最大能连续的覆盖到j,然后f[i]->f[j] O(n^2)
对于两边的情况呢。。?
每个圆覆盖的不再是一个连续的区间了。。但是把点分成上下两半来看,每边的圆覆盖的一定还是一个连续的区间
本来我们是一个区间直接转移的。。现在区间要划分之后才连续了。。
我们不妨在状态里存一下最后一个区间,一个点一个点转移
f[i][j][k]表示考虑到了第i个点,上面用的最后一个圆是j,下面用的最后一个圆是k的代价
如果i+1在j或者k内,直接转移
否则从上面或者下面新选一个圆,新开一个区间转移
那么这题就解决啦> <
总结一下的话,就是证明了一个性质:可以分配使得每个圆覆盖的连续之后,我们就可以在每次前一个圆不能覆盖了之后,选一个新的圆并且把原来的圆丢弃了(所以一个点要不要选新圆就只和上一个圆有关了)
证明的方法是,考察那个新圆之前的圆(不能覆盖当前的x=a这个点的===>要么x=a右侧被新圆完全覆盖,要么x=a左侧被新院完全覆盖),然后就得到要么以后都不会用到之前的圆,要么以前不需要用到之前的圆,那么覆盖就连续了。。
4
2016
HNSDFZ集训的notes
窝记了70+条来着。。?窝决定搞完一个note发一个到这里!
欢迎大家催更 > <
当前进度 :8.5/70
1.如果要找到二维矩形内所有点(k个),归并树(log^2n + k)比主席树(klogn。。线段树找到在哪些x坐标上有点,对每个x坐标开一个vector,然后在每个有点的vector里面二分一下)优。。
//find kth
x = S = 0;
dep(i,m,0){
x ^= 1 << i;
if (x < N && S + s[x] < k) //x <= N! 一定要记得判一下!
S += s[x];
else
x ^= 1 << i;
}
x++;
11.C(n,2)种约束(若干个不等),无法容斥,
似乎是dp一下找出n个点、j个联通块方案数对答案的贡献之类的。。。。?
16
2015
CC CNTDSETS
首先中文题面错了,是切比雪夫距离,而不是曼哈顿距离
切比雪夫距离的话,我们就强制每个维度上都必须要有一个取到0点,注意若干个面必须有一个取到0没有若干个面都没有取到0好做,那么直接容斥转化为后者即可。
#include <iostream>
#include <cstdio>
#include <algorithm>
#define dep(i,a,b) for(int i = a; i >= b; i--)
#define rep(i,a,b) for(int i = a; i <= b; i++)
using namespace std;
const int M = 1000000007;
int pow(int a, int b, int c){
int w = 1;
for(;b;b >>= 1, a = 1LL * a * a % c) if (b & 1) w = 1LL * w * a % c;
return w;
}
const int N = 1010;
int fac[N], inv[N];
int c(int n, int m){
return 1LL * fac[n] * inv[m] % M * inv[n - m] % M;
}
int n;
int calc(int d){
if (d == 0) return 1;
int ans = 0, t = 1;
rep(i,0,n){
int tmp = 1LL * c(n,i) * pow(2, 1LL * pow(d, i, M - 1) * pow(d + 1, n - i, M - 1) % (M - 1), M) % M;
ans += t * tmp, ans %= M;
t = -t;
}
return ans;
}
void work(){
int d; scanf("%d%d",&n,&d);
int ans = (calc(d) - calc(d - 1)) % M;
if (ans < 0) ans += M;
printf("%d\n",ans);
}
int main(){
fac[0] = 1; rep(i,1,1000) fac[i] = 1LL * fac[i - 1] * i % M;
inv[1000] = pow(fac[1000], M - 2, M); dep(i,1000,1) inv[i - 1] = 1LL * inv[i] * i % M;
int T; scanf("%d",&T);
while (T--) work();
}
23
2015
ahoi2015 (jsoi round2) 滚粗记
Day1之前学习了怎么配置gedit和对拍,在比赛里帮了自己大忙……
比赛的时候就用gedit的经典蓝色配色写的代码……自己配置了一键编译
Day1:
早上随便吃了一点就上了考场,想多带点水,最后还是只带了两瓶
于是最后没水喝好难受啊……
t1使劲画了画样例,怎么都画不对……就弃疗了
结果大家最后直接找规律A了……真是遗憾
回来之后我一直在抱怨自己……直到看见神犇说“自己技不如人啊”才反应过来……我是不该抱怨的
只能说自己在考场上放弃t1去写t3一个没有把握的做法是轻率的
同时t3的做法似乎写挂了,只有40,说明自己的代(mo)码(ban)能力还是要提高啊……
然后二分答案做了t2正解,对拍找到了一个错误之后,拍了好几下都过了,然后居然乱调,浪费了很长时间。感觉心态有两个“诶呀,对拍调参又轻松又好玩,还是在干正事”呵呵……省选是去玩的吗……感觉这个心态和自己做作业偷偷玩手机的心态差不多啊 ……就是偷懒安慰自己罢了。另外一个心态就是“只要A了一题就差不多了吧,反正js的题一向很难”,呵呵,你会做 别人就不会?怎么可能!你必须自己尽力拿分啊。
最后知道Day1成绩的时候十分悲伤……埋怨自己……
Day2:
Day1的教训之后态度认真了不少
但是早上起来早了好困啊……好困好困好困啊……
被bkq等学长说“数学差”……很是不服
打开t1之后,发现是期望题……有了“证明自己数学不差”的想法
然后注意到其实某个女孩子选择某个男孩的概率是确定的,等比数列求之……
之后期望可加就直接做了……
写了个暴力和BIT拍……似乎一次就拍过了
拍过了不敢耽误就去看t2了
又有了“诶呀A了一题就行了吧”的想法……真是可恶!
然后发现t2首先可以费用流,感觉数据范围像是贪心……于是yy了一个靠谱的,脑补了下大致证明……
然后和费用流拍过了……但是复杂度比较高……(但是已经有70分了)
感觉脑子不清醒了,发现t3 40分似乎可写,t2剩下的30就算了吧(以为是要写个splay或者是用set什么的)……
纠结了一会三角函数把t3 40分写出来了……发现好像没处理y1<0的情况……又纠结半天,写出来了……
手动画数据调了调就不管了
仔细想想,发现t2那30分一个priority_queue就搞定了,然后愉快的写了,对拍出一个错误
然后拍过了……怕有问题,于是
if (n<=200) work1(); else if (n<=1000) work2(); else work3();
我把三个版本并到一起了……
然后特意留意了一下空间,确定不会MLE
最后对拍的时候不小心弄错了版本,结果WA半天,虚惊一场
然后比赛就结束了,十分惋惜的说,如果d1t1做出来了就无悬念A队了吧
最后省队肯定是进了,但是不知道能不能进A队
第一天拿着手机在qq上找别人帮我看成绩,结果是0+100+40=140……跪的很惨……3位芜湖大爷ak了
第二天打电话问老师也没有,最后还是day1 ak的芜湖大爷罗教帮我看的……100+100+40=240 也算没有失误了 和芜湖大爷并列rank2
最后总结:
1.比赛心态很重要,时刻记得保证基本分,多想想,所有题都要看懂,都要想……
2.比赛的时候千万不能有懒惰的想法,对拍的时候可以看题,不要偷懒
3.尽人事,听天命。
Update:
Day1t3我是树链剖分+主席树的……树链剖分是为了提取出一条路径……然而……taorunz大爷告诉我……这个信息是支持加法减法的,也就是可以s(u)+s(v)-2*s(lca)……多显然的结论啊……我居然注意到…看来考场上还是要多想想啊……TAT
